Tổng hợp kiến thức toán 12 được đánh giá là các kiến thức quan trọng mà bạn nên nắm để giải quyết các vấn đề việc bổ sung các kiến thức này luôn cần thiết cho quá trình học. Vì vậy trong phần nội dung bài viết này chúng tôi sẽ giới thiệu cho bạn về Tổng hợp kiến thức toán 12 chính xác.
Tổng hợp kiến thức toán 12 là một trong những môn học chính trong chương trình giáo dục phổ thông tại Việt Nam. Đây không chỉ là cấp học cuối cùng của bậc phổ thông mà còn là bước đệm quan trọng cho học sinh trước khi bước vào giai đoạn học tập cao hơn. Mục tiêu chính của môn Toán 12 là giúp học sinh củng cố và phát triển những kiến thức và kỹ năng đã học ở các khối lớp trước, đồng thời trang bị cho học sinh khả năng vận dụng các khái niệm toán học trong thực tế. Điều này không chỉ có ý nghĩa trong việc đạt được điểm cao trong các kỳ thi mà còn cho cả sự phát triển tư duy logic và khả năng giải quyết vấn đề.
Giới thiệu về Toán 12
Kiến thức Toán học trong lớp 12 bao gồm nhiều chủ đề quan trọng như đại số, hình học, giải tích và xác suất thống kê. Những chủ đề này không chỉ giúp học sinh nắm vững kiến thức cơ bản mà còn hỗ trợ họ trong việc thực hiện các bài kiểm tra và kỳ thi quan trọng, đặc biệt là kỳ thi Quốc gia. Sự thành thạo trong môn Toán sẽ mở ra nhiều cơ hội cho học sinh trong ngành nghề mà họ lựa chọn trong tương lai. Hơn nữa, Toán học cũng là ngôn ngữ chung của khoa học, vì vậy những ai có nền tảng vững chắc sẽ có lợi thế khi theo đuổi các lĩnh vực như kỹ thuật, khoa học tự nhiên và công nghệ thông tin.
Với những lợi ích to lớn mà môn Toán lớp 12 mang lại, học sinh cần có sự chuẩn bị nghiêm túc và chiến lược ôn tập hiệu quả. Việc nghiên cứu và thực hành các bài tập mẫu, kết hợp với việc tham khảo sách giáo khoa và tài liệu bổ sung sẽ giúp học sinh nắm vững kiến thức và tự tin hơn trong các kỳ thi sắp tới. Chương trình Toán 12 không chỉ là một môn học mà còn là một hành trang giúp học sinh vững bước trên con đường học vấn sau này.
Các chủ đề chính trong Toán 12
Trong chương trình Toán lớp 12, học sinh sẽ tiếp cận nhiều chủ đề khác nhau, bao gồm Đại số, Hình học, Tổ hợp xác suất, và Giải tích. Mỗi chủ đề này không chỉ phản ánh kiến thức nền tảng mà còn giúp học sinh phát triển kỹ năng tư duy logíc và giải quyết vấn đề trong nhiều ngữ cảnh khác nhau.
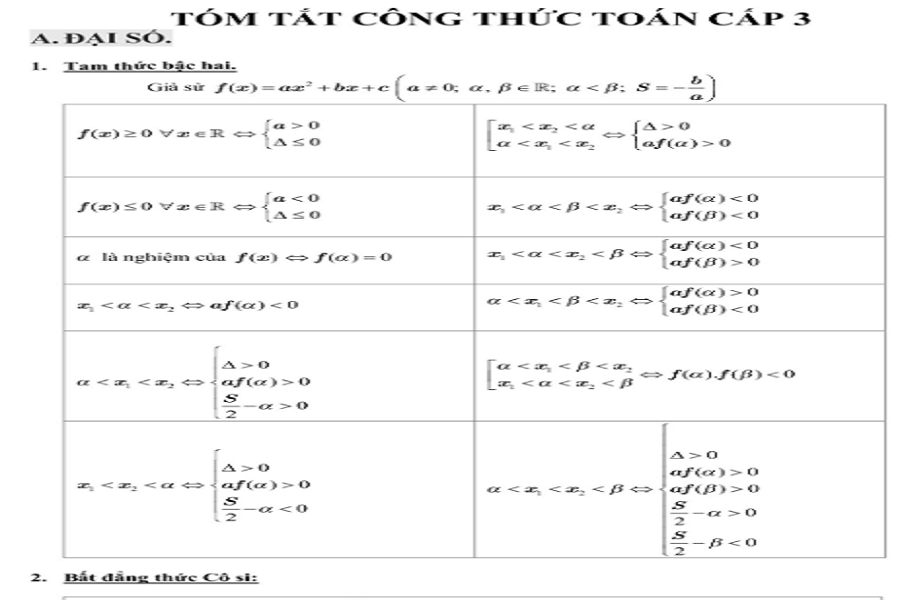
Chủ đề Đại số chủ yếu tập trung vào các khái niệm như hàm số, bất phương trình và hệ phương trình. Học sinh sẽ được hướng dẫn cách biểu diễn và phân tích các hàm số đa thức, đồng thời tìm hiểu về bản chất của các điểm cực trị và sự biến thiên của hàm. Những kiến thức này không chỉ giúp các em trong việc giải quyết bài tập mà còn tạo tiền đề cho các môn học cao hơn.
Trong khi đó, Hình học cung cấp cho học sinh kiến thức về hình học phẳng và hình học không gian. Học sinh sẽ được học cách tính diện tích, thể tích, cũng như các tính chất của các hình khối như hình cầu, hình hộp và hình chóp. Việc hiểu rõ các định lý và hệ quả trong Hình học sẽ giúp ích rất nhiều cho việc tư duy trực quan cũng như làm bài trong kỳ thi.
Chủ đề Tổ hợp xác suất mang đến những khái niệm cơ bản về xác suất, biến cố, và các phương pháp thống kê, giúp học sinh phát triển khả năng phân tích và lập luận. Điều này đặc biệt quan trọng trong việc ra quyết định dựa trên các thông tin không chắc chắn.
Cuối cùng, Giải tích sẽ đưa học sinh vào thế giới của đạo hàm và tích phân, giúp các em hiểu rõ hơn về cách tính toán các tỷ lệ thay đổi và các diện tích dưới đường cong. Mỗi chủ đề trong chương trình Toán lớp 12 đều có vai trò quan trọng trong việc xây dựng nền tảng kiến thức vững chắc cho học sinh, chuẩn bị cho các kỳ thi đại học và nghề nghiệp trong tương lai.
Bài viết đáng xem : Tổng hợp kiến thức Toán lớp 10
Đại số và các bài toán liên quan
Đại số là một trong những bộ phận quan trọng của chương trình Toán học lớp 12, bao gồm các khái niệm như hàm số, phương trình và bất phương trình. Hiểu rõ các khái niệm này là rất cần thiết để học sinh có thể giải quyết các bài tập một cách hiệu quả và chính xác. Đầu tiên, hàm số được định nghĩa là quy luật kết nối giữa các biến, trong đó một đầu vào sẽ cho ra đầu ra tương ứng. Học sinh cần nắm vững các loại hàm số khác nhau, bao gồm hàm số bậc nhất, bậc hai, và hàm số đa thức.
Tiếp theo, phương trình là một mệnh đề toán học mà trong đó có dấu “=” theo cả hai phía. Các dạng phương trình thường gặp bao gồm phương trình bậc nhất, bậc hai và phương trình lượng giác. Để giải các phương trình này, học sinh cần biết các phương pháp như phân tích nhân tử, công thức nghiệm và phương pháp thế. Mỗi dạng phương trình lại có những kỹ thuật giải riêng, do đó việc luyện tập thường xuyên là rất quan trọng.
Bất phương trình cũng không kém phần quan trọng trong đại số. Một bất phương trình được định nghĩa là một mệnh đề mà trong đó có dấu không bằng. Học sinh cần phải tìm ra tập nghiệm của bất phương trình và biểu diễn nó trên trục số. Thấu hiểu cách vẽ đồ thị và phân tích các trường hợp riêng biệt sẽ giúp các em nhanh chóng tìm ra các nghiệm của bất phương trình. Để đạt được kết quả cao trong phần này, hãy chú ý đến các dạng bài tập thường gặp và thực hành thường xuyên, đồng thời nhớ làm quen với các lưu ý quan trọng như dấu của các nghiệm hay cách thức chuyển chuyển bất phương trình.
Hình học: Các kiến thức cần nắm vững
Trong chương trình Toán 12, hình học đóng một vai trò quan trọng không chỉ trong kỳ thi mà còn trong việc phát triển tư duy logic. Cần nắm vững hai nhánh chính của hình học là hình học phẳng và hình học không gian. Hình học phẳng thường xoay quanh các khái niệm như tam giác, hình chữ nhật, hình tròn, và các định lý liên quan đến chúng. Học sinh cần nắm vững các định lý nổi bật như định lý Pitago, định lý về các góc trong tam giác hay định lý về tổng các góc của một đa giác, vì đây là cơ sở để giải quyết nhiều bài toán hơn trong đời sống thực.
Bên cạnh đó, hình học không gian cũng rất quan trọng, với các khái niệm như khối đa diện, hình cầu, và hình trụ. Học sinh cần hiểu rõ tính chất và cách tính diện tích bề mặt cũng như thể tích của các hình khối này. Ví dụ, thể tích của hình trụ được tính bằng công thức V = πr²h, trong đó r là bán kính của đáy và h là chiều cao. Phần kiến thức này giúp học sinh giải quyết các bài toán liên quan đến hình học 3 chiều, một lĩnh vực rất thường gặp trong bài thi tốt nghiệp.
Các đinh lý và định nghĩa là nền tảng cho việc vận dụng lý thuyết vào thực tế. Để học hiệu quả, học sinh nên thực hành giải nhiều dạng bài tập để nâng cao kỹ năng nhận diện hình học và áp dụng các kiến thức đã học vào các bài toán cụ thể. Việc nắm rõ các khái niệm và định nghĩa sẽ giúp học sinh không chỉ trong kỳ thi, mà còn trong việc áp dụng toán học vào các lĩnh vực khác trong cuộc sống hàng ngày.
Tổ hợp và xác suất: Áp dụng thực tế
Tổ hợp và xác suất là hai khái niệm toán học cơ bản nhưng rất quan trọng trong việc giải quyết các bài toán thực tế. Tổ hợp đề cập đến việc lựa chọn các phần tử từ một tập hợp mà không xét đến thứ tự, trong khi xác suất đo lường khả năng xảy ra của một sự kiện cụ thể. Việc hiểu rõ những khái niệm này có thể giúp học sinh trong việc phân tích và đưa ra những quyết định hợp lý hơn trong cuộc sống hàng ngày cũng như trong các bài toán vật lý hay thống kê.
Các công thức tổ hợp thường được sử dụng như C(n, k) = n! / (k! * (n-k)!), trong đó n là tổng số phần tử và k là số phần tử được chọn. Công thức này cho phép chúng ta tính toán số lượng cách chọn k phần tử từ n phần tử mà không cần quan tâm đến thứ tự. Từ đó, học sinh có thể ứng dụng vào nhiều tình huống thực tế, chẳng hạn như trong việc lên kế hoạch cho các hoạt động nhóm, hay trong các cuộc thi để tạo ra các đội chơi có sự cân bằng về kỹ năng.
Xác suất cũng rất đa dạng trong ứng dụng của nó. Chẳng hạn, việc tính xác suất xảy ra của một sự kiện có thể được thực hiện bằng cách sử dụng công thức P(A) = k/n, trong đó k là số trường hợp thuận lợi và n là tổng số trường hợp có thể xảy ra. Những bài toán điển hình có thể bao gồm tính xác suất về việc rút thẻ, tung đồng xu hay các trò chơi quay số. Các bài toán này không chỉ giúp học sinh giải quyết bài toán một cách chính xác mà còn có thể áp dụng vào các lĩnh vực như tài chính, y tế, và nghiên cứu xã hội, phát triển kỹ năng phân tích và tư duy phản biện.

