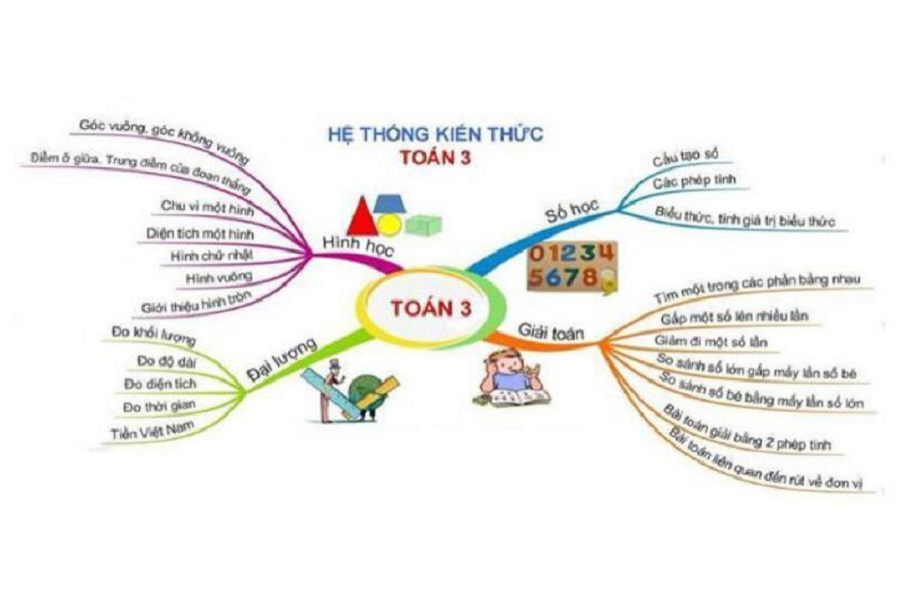
Kiến thức toán lớp 3 là nền tảng kiến thức cơ bản trong cấp bậc tiểu học nó giúp bạn dễ dàng hoàn thành chương trình học sau này khi đã nắm được các kiến thức cơ bản này. Vì vậy trong phần nội dung bài viết này chúng tôi xin nói về những Kiến thức toán lớp 3 cần nắm
Trong Kiến thức toán lớp 3 , việc nắm vững các khái niệm toán học cơ bản là rất quan trọng để tạo nền tảng cho những kiến thức phức tạp hơn sau này. Một trong những khái niệm đầu tiên mà học sinh cần hiểu là các phép toán cơ bản, bao gồm cộng, trừ, nhân, và chia. Những phép toán này không chỉ cung cấp cách thức để thực hiện các tính toán mà còn giúp học sinh phát triển tư duy logic và khả năng giải quyết vấn đề.
Các Khái Niệm Toán Học Cơ Bản
Các phép cộng và trừ là hai thao tác cơ bản mà học sinh thường xuyên gặp trong các bài tập. Ví dụ, khi cộng hai số tự nhiên như 3 và 5, học sinh sẽ có kết quả là 8. Tương tự, phép trừ sẽ giúp họ tìm ra sự khác biệt giữa hai số, ví dụ như 10 trừ 4 sẽ cho kết quả là 6. Những phép toán này đơn giản nhưng rất quan trọng trong đời sống hàng ngày cũng như trong các bài toán khác.
Bên cạnh cộng và trừ, nhân và chia cũng đóng vai trò quan trọng trong toán học cơ bản. Phép nhân được sử dụng để tính toán với số lượng lớn, ví dụ, 4 nhân 3 là 12, giúp học sinh hiểu được khái niệm về số lượng và nhân đôi. Phép chia, mặt khác, giúp họ phân chia một số thành các phần bằng nhau, chẳng hạn như 12 chia cho 3 sẽ cho ra 4, thể hiện cách thức phân chia và xử lý dữ liệu.
Các khái niệm về số tự nhiên và số nguyên cũng cần được duy trì. Số tự nhiên bao gồm tất cả các số dương, trong khi số nguyên không chỉ bao gồm số tự nhiên mà còn cả số 0 và số âm. Lớp 3 sẽ giúp học sinh làm quen với cách thực hiện các phép toán với những loại số này. Thực hành là một phần không thể thiếu trong việc học toán. Các bài tập thực hành sẽ giúp củng cố lý thuyết và hỗ trợ học sinh áp dụng kiến thức vào thực tiễn.
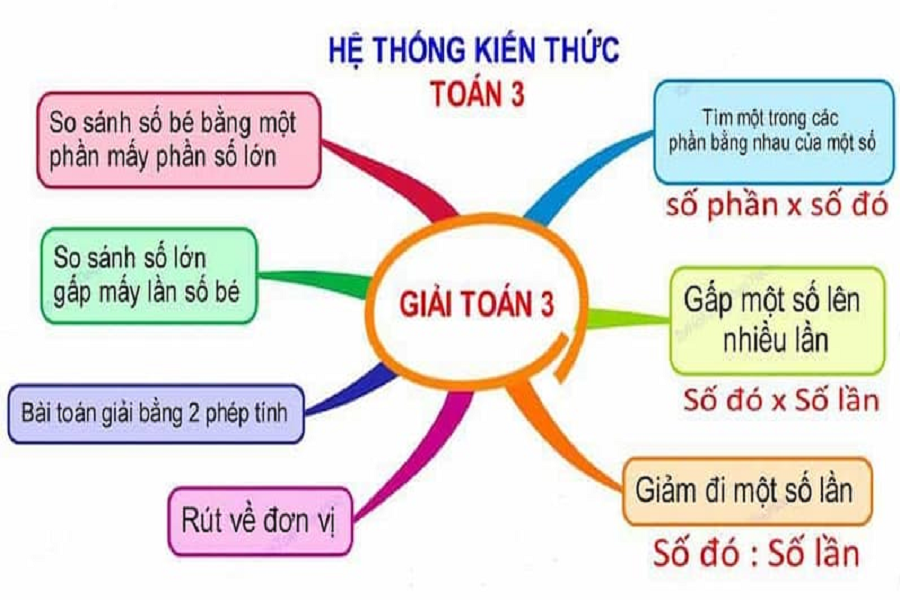
Hình Học và Các Đối Tượng Hình Học
Hình học là một nhánh của toán học, tập trung vào nghiên cứu các hình dạng và không gian. Các đối tượng hình học cơ bản bao gồm điểm, đường thẳng, đoạn thẳng, hình vuông, hình chữ nhật và hình tròn. Mỗi đối tượng này có đặc điểm riêng và đóng một vai trò quan trọng trong việc phát triển tư duy logic của học sinh. Điểm là đơn vị cơ bản trong hình học, không có chiều dài, chiều rộng hay chiều cao. Đường thẳng thì kéo dài vô hạn về cả hai phía mà không bị uốn cong. Đoạn thẳng, ngược lại, có độ dài xác định, là phần của đường thẳng giữa hai điểm.
Trong khi đó, hình vuông và hình chữ nhật là hai loại hình tứ giác với nhiều ứng dụng trong thực tế. Hình vuông có bốn cạnh bằng nhau, và các góc vuông tạo nên tính đối xứng cao. Hình chữ nhật cũng có bốn góc vuông, nhưng các cạnh đối diện có chiều dài khác nhau. Cả hai loại hình này đều được dùng rộng rãi trong xây dựng, kiến trúc và thiết kế nội thất. Hình tròn, với đặc điểm nổi bật là không có góc, được xác định qua bán kính và đường kính, có ứng dụng quan trọng trong các lĩnh vực như cơ học và kỹ thuật.
Để đo độ dài của các đoạn thẳng, học sinh có thể sử dụng thước kẻ, trong khi diện tích của hình vuông và hình chữ nhật được tính bằng công thức đơn giản: chiều dài nhân với chiều rộng. Cụ thể, diện tích hình vuông là cạnh nhân với cạnh, còn diện tích hình chữ nhật là dài nhân rộng. Đối với hình tròn, diện tích được tính bằng công thức π nhân với bán kính bình phương. Hình học không chỉ hỗ trợ các khái niệm cơ bản trong học thuật mà còn giúp học sinh hiểu rõ hơn về môi trường xung quanh mình qua các bài tập thực hành và hình ảnh minh họa.
Bài viết đáng xem : Kiến thức tiếng anh
Giải Bài Tập Toán Lớp 3: Chiến Lược và Kỹ Năng
Để phát triển kỹ năng giải bài tập toán lớp 3, học sinh cần được trang bị các chiến lược cần thiết giúp họ không chỉ làm quen với các dạng bài tập mà còn tìm ra lời giải một cách hiệu quả. Một trong những chiến lược quan trọng nhất là phân tích đề bài. Việc hiểu rõ yêu cầu của đề bài sẽ giúp học sinh xác định được thông tin cần thiết và hướng đi cho quá trình giải quyết vấn đề.
Khi tiếp cận một bài toán, học sinh nên đọc kỹ từng câu, ghi chú lại những thông tin quan trọng, và xác định câu hỏi cụ thể mà đề bài yêu cầu trả lời. Ví dụ, khi đọc một bài toán về số lượng quả, học sinh cần lưu ý các con số đưa ra, các phép toán cần thực hiện và đặc biệt là câu hỏi cuối cùng. Bước phân tích này không chỉ làm rõ nội dung mà còn tạo nền tảng vững chắc cho các bước tiếp theo.
Sau khi đã hiểu rõ đề bài, học sinh có thể áp dụng kỹ năng “dây chuyền khai thác thông tin”. Nghĩa là, từ các thông tin đã có, học sinh sẽ lần lượt thực hiện các phép toán, mỗi bước dẫn dắt đến bước tiếp theo, cho đến khi tìm ra được lời giải. Quy trình này không chỉ giúp tổ chức thông tin một cách có hệ thống mà còn giúp học sinh tự tin hơn qua từng bước giải.
Thực hành là phần không thể thiếu trong quá trình này. Các bài tập thực hành đa dạng sẽ giúp học sinh làm quen với nhiều kiểu bài cùng với các mức độ khó khác nhau, từ đó củng cố kiến thức và rèn luyện các kỹ năng giải toán. Để hỗ trợ học sinh, giáo viên có thể cung cấp những bài tập điển hình, giải chi tiết từng bước để học sinh tham khảo.