Tổng hợp những kiến thức toán lớp 6 được xem là những kiến thức làm nền tảng sau này để hoàn thành giai đoạn học cần thiết để tạo nền tảng cho công việc sau này. Vì vậy trong bài viết này sẽ giới thiệu về Tổng hợp những kiến thức toán lớp 6 mà bạn cần nắm.
Tổng hợp những kiến thức toán lớp 6 là một giai đoạn quan trọng trong chương trình giáo dục trung học cơ sở tại Việt Nam. Trong năm học này, học sinh sẽ tiếp cận nhiều khái niệm và công thức toán học cơ bản, đồng thời gây dựng nền tảng vững chắc cho các môn học sau này. Mục tiêu của chương trình toán học lớp 6 không chỉ nhằm cung cấp kiến thức lý thuyết mà còn thúc đẩy khả năng tư duy logic, phân tích và giải quyết vấn đề cho học sinh.
Giới Thiệu Về Toán Lớp 6
Tầm quan trọng của việc học toán trong giai đoạn này không thể phủ nhận. Toán học là một công cụ thiết yếu trong cuộc sống hàng ngày, giúp học sinh khả năng suy luận và tư duy phản biện. Việc nắm vững các khái niệm cơ bản như số học, đại số, hình học và thống kê sẽ giúp học sinh hình thành tư duy kiến thức cao hơn trong những năm học tiếp theo. Điều này cũng tạo ra nền tảng cho các môn học khác, từ khoa học tự nhiên cho đến kinh tế học.
Trong chương trình toán học lớp 6, học sinh sẽ làm quen với nhiều chủ đề quan trọng, bao gồm số tự nhiên, phân số, thập phân, tỷ lệ, và tính diện tích, thể tích của các hình khối cơ bản. Thêm vào đó, học sinh sẽ được phân tích các bài toán thực tế, từ đó phát triển khả năng áp dụng kiến thức toán trong thực tế. Những điều này không chỉ giúp củng cố kiến thức mà còn khơi dậy hứng thú học tập, mở ra cánh cửa đến với các khái niệm phức tạp hơn trong tương lai.
Số Học Cơ Bản
Số học là một nhánh quan trọng trong toán học, đóng vai trò nền tảng cho nhiều lĩnh vực khác nhau. Trong lớp 6, học sinh sẽ được giới thiệu và tìm hiểu về các loại số cơ bản bao gồm số tự nhiên, số nguyên và số thập phân. Mỗi loại số có những đặc điểm và cách sử dụng riêng biệt, tạo ra sự đa dạng trong việc thực hiện các phép toán.
Số tự nhiên là tập hợp các số từ 0 trở đi như 0, 1, 2, 3,… Chúng được sử dụng để đếm và lập danh sách. Số tự nhiên không bao gồm các số âm hay số thập phân. Bên cạnh đó, số nguyên mở rộng khái niệm của số tự nhiên bằng cách bao gồm cả các số âm, như -3, -2, -1, 0, 1, 2, 3,… Số nguyên cho phép chúng ta thực hiện các phép toán phức tạp hơn, chẳng hạn như phép trừ và các phép toán liên quan đến các giá trị âm.
Số thập phân, như 0.5, 1.25, hay -3.75, là những số mà phần thập phân của chúng được ngăn cách bởi dấu phẩy, thể hiện giá trị nhấp nháy giữa các số nguyên. Việc hiểu và sử dụng số thập phân là rất cần thiết trong cuộc sống hàng ngày cũng như trong các tình huống tính toán phức tạp. Học sinh cũng sẽ tìm hiểu cách thực hiện các phép toán cơ bản như cộng, trừ, nhân và chia với các loại số này.
Như vậy, số học cơ bản cung cấp nền tảng vững chắc cho học sinh trong việc khám phá toán học ở các cấp độ cao hơn. Sự thành thạo trong các phép toán cơ bản với số tự nhiên, số nguyên, và số thập phân sẽ giúp học sinh tự tin hơn trong việc giải quyết các bài toán trong thực tế.
Phân Số và Số Thập Phân
Phân số và số thập phân là hai khái niệm quan trọng trong chương trình toán học lớp 6. Phân số được định nghĩa là một phần của một tổng thể, thể hiện mối quan hệ giữa hai số nguyên, trong đó số ở trên (tử số) biểu thị phần được tính đến, và số ở dưới (mẫu số) biểu thị tổng số phần của tổng thể đó. Ví dụ, phân số 3/4 biểu thị rằng có ba phần trong tổng số bốn phần.
Số thập phân, ngược lại, là cách biểu diễn phân số dưới dạng hệ thống số có mũ 10, thường sử dụng dấu phẩy để ngăn cách phần nguyên và phần thập phân. Chẳng hạn, 0.75 là số thập phân tương ứng với phân số 3/4. Sự chuyển đổi giữa hai hình thức này rất quan trọng, bởi nó giúp học sinh nắm vững cách biểu diễn và thực hiện các phép toán một cách linh hoạt hơn.
Các phép toán liên quan đến phân số và số thập phân bao gồm cộng, trừ, nhân và chia. Đối với phân số, việc thực hiện các phép toán thường yêu cầu đưa về mẫu số chung trong các phép cộng và trừ. Trong khi đó, số thập phân cho phép việc tính toán diễn ra dễ dàng hơn nhờ vào tính chất của hệ thống cơ số 10. Học sinh có thể dễ dàng cộng hoặc trừ các số thập phân bằng cách sắp xếp chúng theo chiều thẳng đứng.
Ứng dụng thực tế của phân số và số thập phân rất rộng rãi trong cuộc sống hàng ngày, từ việc tính toán chi phí khi mua sắm đến việc đo lường chiều dài, trọng lượng hay thời gian. Khi nắm vững kiến thức về phân số và số thập phân, học sinh sẽ phát triển kỹ năng toán học cần thiết để giải quyết các vấn đề thực tiễn và nâng cao khả năng tư duy logic của mình.
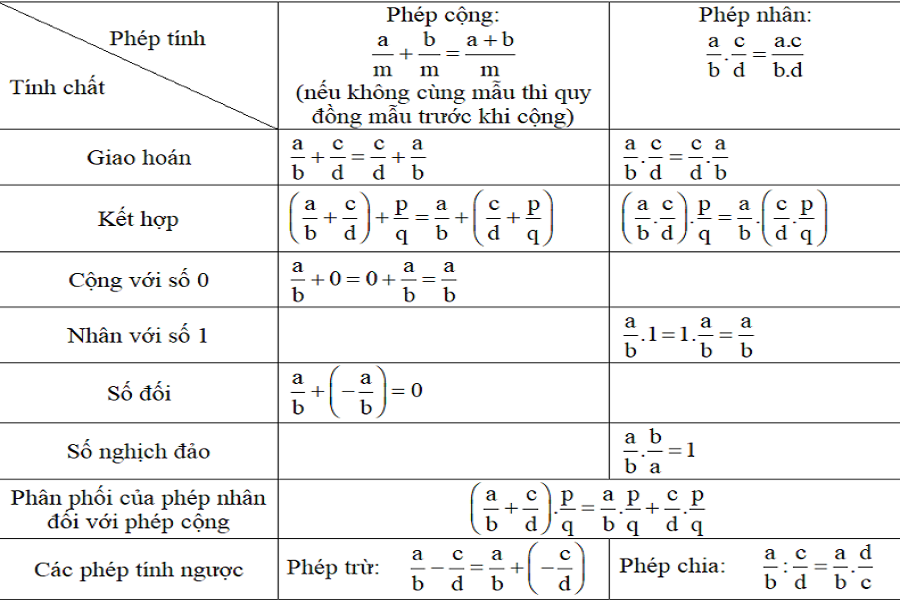
Đại Số Căn Bản
Đại số là một nhánh quan trọng trong toán học, không chỉ mang lại giải pháp cho các vấn đề lý thuyết mà còn hỗ trợ giải quyết nhiều bài toán thực tiễn. Trong phần này, chúng ta sẽ tìm hiểu các khái niệm cơ bản về đại số, bao gồm biến, biểu thức đại số và phương trình cùng với cách giải các phương trình đơn giản.
Biến là một đại lượng không cố định, thường được ký hiệu bằng một hay nhiều chữ cái, như x, y hoặc z. Biến cho phép chúng ta biểu diễn các giá trị có thể thay đổi và là thành phần nền tảng của bất kỳ biểu thức đại số nào. Biểu thức đại số là sự kết hợp của các hằng số, biến, cũng như các phép toán như cộng, trừ, nhân và chia. Ví dụ, biểu thức 2x + 3 là một biểu thức đại số, trong đó 2x là một thành phần đại số và 3 là một hằng số.
Phương trình đại số được hình thành khi hai biểu thức đại số được so sánh bằng nhau, thường được biểu diễn dưới dạng ax + b = c. Để giải phương trình này, chúng ta cần tìm giá trị của biến để phương trình trở nên đúng. Cách giải đơn giản nhất là biến đổi phương trình về dạng x = (c – b) / a nếu a khác không. Điều này cho phép người học nhận biết được mối quan hệ giữa các biến trong các tình huống thực tế khác nhau.
Ứng dụng của đại số rất đa dạng, từ việc tính toán tài chính đến việc giải quyết các vấn đề về hình học và phân tích dữ liệu. Đại số không chỉ giúp chúng ta phát triển khả năng tư duy logic mà còn hỗ trợ trong việc tìm ra các giải pháp sáng tạo cho các vấn đề phức tạp trong cuộc sống hàng ngày.
Hình Học Cơ Bản
Trong toán học, hình học cơ bản là một phần quan trọng, đặc biệt trong chương trình học lớp 6. Các khái niệm như điểm, đường thẳng, góc, hình tam giác và hình chữ nhật là những kiến thức cơ bản mà học sinh cần nắm vững. Đầu tiên, một điểm là vị trí có tọa độ xác định trong không gian, không có kích thước hay hình dạng. Điểm được ký hiệu bằng các chữ cái như A, B hay C. Tiếp theo là đường thẳng, đây là tập hợp vô hạn các điểm nằm trên một cùng một mặt phẳng và có chiều dài không xác định. Đường thẳng được ký hiệu bởi hai điểm nằm trên nó, chẳng hạn như AB.
Góc là phần không gian được tạo ra từ hai đường thẳng gặp nhau ở một điểm, gọi là đỉnh. Để đo góc, người ta sử dụng đơn vị độ. Các góc có thể được phân loại theo độ mở của chúng, như góc nhọn, góc vuông và góc tù. Hình tam giác là một trong những hình học cơ bản nhất, được hình thành từ ba điểm không nằm trên cùng một đường thẳng. Tổng của ba góc trong một hình tam giác luôn bằng 180 độ, và có ba loại tam giác dựa vào độ dài các cạnh: tam giác đều, tam giác cân và tam giác vuông.
Hình chữ nhật cũng là một hình học quan trọng, có bốn cạnh và bốn góc vuông. Để tính chu vi, ta sử dụng công thức: Chu vi = 2 (dài + rộng). Diện tích của hình chữ nhật được tính bằng công thức: Diện tích = dài x rộng. Việc nắm vững những khái niệm hình học cơ bản này không chỉ giúp học sinh thực hành tốt mà còn là nền tảng cho các kiến thức phức tạp hơn trong tương lai.
Bài viết đáng xem : Tổng hợp kiến thức hóa học 12
Tỉ Số và Tỉ Lệ
Tỉ số và tỉ lệ là hai khái niệm cơ bản trong toán học lớp 6, thường xuất hiện trong các bài toán thực tiễn. Tỉ số được định nghĩa là một mối quan hệ giữa hai đại lượng, thể hiện tỷ lệ của chúng thông qua một phép chia. Ví dụ, nếu có 8 quả táo và 4 quả chuối, tỉ số giữa táo và chuối là 8:4, có thể đơn giản hóa thành 2:1. Điều này cho thấy rằng số lượng táo gấp đôi số lượng chuối.
Ngược lại, tỉ lệ là một cách so sánh giữa hai tỉ số. Nếu tỉ số giữa chiều cao của một cây và chiều cao của một người là 3:1, điều này có nghĩa là nếu người đó cao 1 mét thì cây cao 3 mét. Tỉ lệ giúp chúng ta hiểu cách một đại lượng này thay đổi so với đại lượng khác. Để áp dụng tỉ lệ trong thực tế, học sinh có thể gặp các tình huống như quy đổi đơn vị, tính toán diện tích hoặc thể tích, hay trong các bài toán liên quan đến tỷ lệ phần trăm.
Các bước tính tỉ số và tỉ lệ rất quan trọng. Một trong những cách tính tỉ số đơn giản là chia số lượng của đại lượng này cho đại lượng kia. Tỉ lệ thường được biết đến qua công thức: tỉ lệ = tỉ số/ 100. Việc tính toán tỉ lệ đúng cách sẽ giúp học sinh phân tích và so sánh dữ liệu, từ đó giải quyết được các bài toán một cách hiệu quả.
Sự hiểu biết về tỉ số và tỉ lệ không chỉ hữu ích trong học tập mà còn rất cần thiết trong cuộc sống hàng ngày. Ví dụ, khi mua sắm, việc so sánh giá cả giữa các sản phẩm khác nhau dựa trên tỉ lệ giá thành sẽ giúp người tiêu dùng đưa ra sự lựa chọn hợp lý hơn.

